[토질및기초] 지반내응력, 구형(직사각형) 등분포하중에 의한 연직응력증가량, Newmark 방법, 구형분할법, 중첩의 원리
지반내 응력
1. 구형(직사각형) 등분포하중이 작용하는 경우
(1) Newmark 방법(구형분할법, 중첩의 원리)
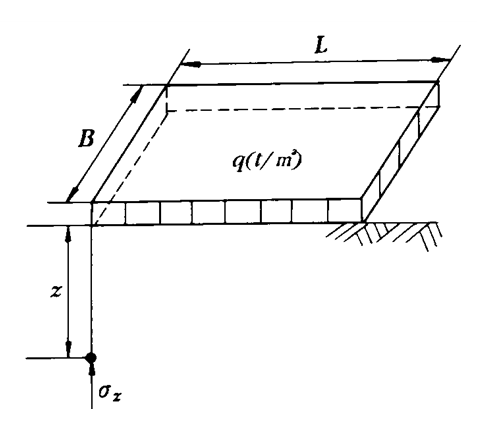
※ 여기서 구형은 공모양의 구가 아니라 직사각형을 의미한다.
① 구형(직사각형) 등분포 하중에 의한 연직응력 증가량 산정식
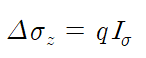
여기서, $\Delta \sigma_z$ : 구형 등분포 하중만에 의한 연직응력 증가량
$q$ : 구형 등분포 하중의 크기
$I_{\sigma}$ : 영향계수(구형 등분포하중의 모서리에서만 영향계수를 구할 수 있다.)

여기서, $B$ : 구형 등분포 하중의 폭
$L$ : 구형 등분포 하중의 길이
$Z$ : 지표면으로부터 연직응력 증가량을 구하고자 하는 점까지의 연직깊이
② 영향계수($I_{\sigma}$) 산정 방법
㉮ 구형 등분포 하중의 모서리가 아닌 점에 대해서는 구형(직사각형) 분할을 하여 그 점(연직응력 증가량을 구하고자 하는 점)을 등분포하중의 모서리에 일치되도록 하여 중첩의 원리를 적용해서 연직응력 증가량을 구한다.
㉯ 영향계수($I_{\sigma}$) 산정
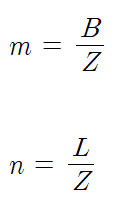
$m$과 $n$을 계산하여 도표를 이용해서 영향계수를 산정한다.
③ 구형 등분포 하중에 의한 연직응력 증가량 산정
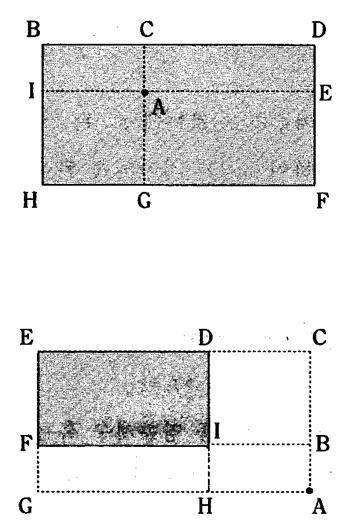
㉮ 연직응력의 증가량을 구하고자 하는 점이 등분포하중 내부에 있는 경우

㉯ 연직응력의 증가량을 구하고자 하는 점이 등분포하중 외부에 있는 경우
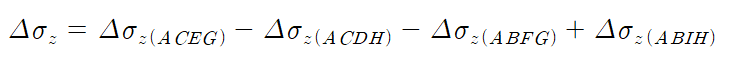
핵심예제
동일한 등분포하중이 작용하는 그림과 같은 (A)와 (B) 두 개의 구형 기초 판에서 A와 B점의 수직 $z$되는 길이에서 증가되는 지중응력을 각각 $\sigma_A$, $\sigma_B$라 할 때 다음 중 옳은 것은? (단, 지반 흙의 성질은 동일하다.)
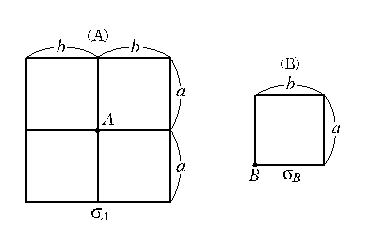
① $\sigma_A = \dfrac{1}{2}\sigma_B$
② $\sigma_A = \dfrac{1}{4}\sigma_B$
③ $\sigma_A = 2\sigma_B$
④ $\sigma_A = 4\sigma_B$
해설
직사각형 등분포하중 모서리 직하의 깊이 $z$되는 점에서의 연직응력 증가량
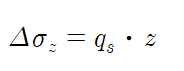
A점에서의 연직응력 증가량은 B점에서의 연직응력 증가량의 4배($\sigma_A = 4\sigma_B$)이다.
정답 ④
토목기사필기 및 실기시험대비 네이버 스토어팜
케이제이에듀 : 네이버쇼핑 스마트스토어
토목기사 시험 독학 완벽 준비
smartstore.naver.com
토목 네이버 엑스퍼트
대학교학습 케이제이에듀 eXpert 프로필 : 네이버 지식iN
엑스퍼트: 토목기사 시험 준비를 도와드립니다
m.expert.naver.com
'토질 및 기초' 카테고리의 다른 글
| [토질및기초] 지반내응력, 접지압, 접촉압력, 가요성기초, 강성기초, 휨성기초, 지반반력, 후팅, contact pressure (0) | 2022.07.08 |
|---|---|
| [토질및기초] 지반내응력, 구형(직사각형) 등분포하중에 의한 연직응력증가량, Kogler 간편법, 2:1 분포법 (0) | 2022.07.07 |
| [토질및기초] 지반내응력, 집중하중에 의한 연직응력증가량, Boussinesq 이론 (0) | 2022.07.05 |
| [토질및기초] 지반내응력, 모세관현상이 발생할 때의 유효응력, 전응력, 간극수압 (0) | 2022.07.04 |
| [토질및기초] 지반내응력, 전응력, 공극수압, 간극수압, 유효응력, 토압계수, 연직전응력, 수평전응력, 연직유효응력, 수평유효응력 (0) | 2022.07.03 |




댓글